Calculus Workbook For Dummies Cheat Sheet

To effectively work through calculus problems, you have to understand a number of topics: the process of evaluating limits, methods of solving various differentiation and integration problems, and the tests for convergence or divergence of infinite series.

Evaluating limits in calculus

The mathematics of limits underlies all of calculus. Limits sort of enable you to zoom in on the graph of a curve — further and further — until it becomes straight. Once it’s straight, you can analyze the curve with regular-old algebra and geometry. That’s the magic of calculus in a very small nutshell.

Here are some important things to remember when evaluating limits:

• The limit at a hole is the height of the hole.
• The limit at infinity is the height of the horizontal asymptote.
• Before trying other techniques, plug in the arrow number. If the result is:
  • A number, you’re done.
  • A number over zero or infinity over zero, the answer is infinity.
  • A number over infinity, the answer is zero.
  • 0/0 or ∞/∞, use L’Hôpital’s Rule.

  

  How to solve differentiation problems

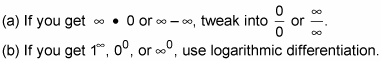
  In calculus, the way you solve a derivative problem depends on what form the problem takes. Common problem types include the chain rule; optimization; position, velocity, and acceleration; and related rates. Here are a few things to remember when solving each type of problem:

  Chain Rule problems

  1. Use the chain rule when the argument of the function you’re differentiating is more than a plain old x.
  2. Work from outside, in.
  3. Don’t touch the inside stuff.
  4. Do only one derivative per step.

  Optimization problems

  1. Express the thing you want to minimize or maximize as a function of the unknown.
  2. Differentiate and set the derivative equal to zero.
  3. Solve and plug the solution into the original function.

  Position, velocity, and acceleration problems

  1. The derivative of position is velocity and the antiderivative of velocity is position.
  2. The derivative of velocity is acceleration and the antiderivative of acceleration is velocity.

  Related rates problems

  1. Assign variables to changing quantities, but not to unchanging things.
  2. Differentiate before plugging in variable values.
  3. Use the Pythagorean Theorem for right triangle problems and use similar triangles for problems involving cones or shapes that have a triangular cross-section.

  Techniques of integration

  You’ll find that there are many ways to solve an integration problem in calculus. The following list contains some handy points to remember when using different integration techniques:

  • Guess and Check. This technique works when the integrand is close to a simple backward derivative.
  • u-substitution. The integration counterpart to the chain rule; use this technique when the argument of the function you’re integrating is more than a simple x.
  • Integration by Parts. Integration’s counterpart to the product rule. 1. Use this technique when the integrand contains a product of functions. 2. Pick your u according to LIATE, box it, “7” it, finish it.
  • Trig Integrals 1. Use Pythagorean identities.

  2. Use half-angle formulas.

  

  

  (or powers of these roots), where a is a constant and u is an expression in x.

  

  

  Solving integration problems

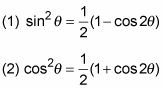
  Calculus riddle: What do the Mean Value Theorem, the Washer and Shell Methods, and the Arc Length and Surface of Revolution formulas have in common? They all involve integration. Integration is very fancy addition. When you solve an integration problem, you take a weird shape whose area you can’t directly determine, then you cut it up into tiny bits whose areas you can determine, and, finally, you add up all these little bits to determine the whole.

  

  Understanding infinite series in calculus

  In calculus, an infinite series is “simply” the adding up of all the terms in an infinite sequence. Despite the fact that you add up an infinite number of terms, some of these series total up to an ordinary finite number. Such series are said to converge. If a series doesn’t converge, it’s said to diverge. Whether a series converges or diverges is one of the first and most important things you will want to determine about the series.

  Here’s a look at various methods you can use to test the convergence or divergence of an infinite series.

  • nth term test: If the nth term of a series doesn’t converge to zero, the series diverges.
  • Geometric series: